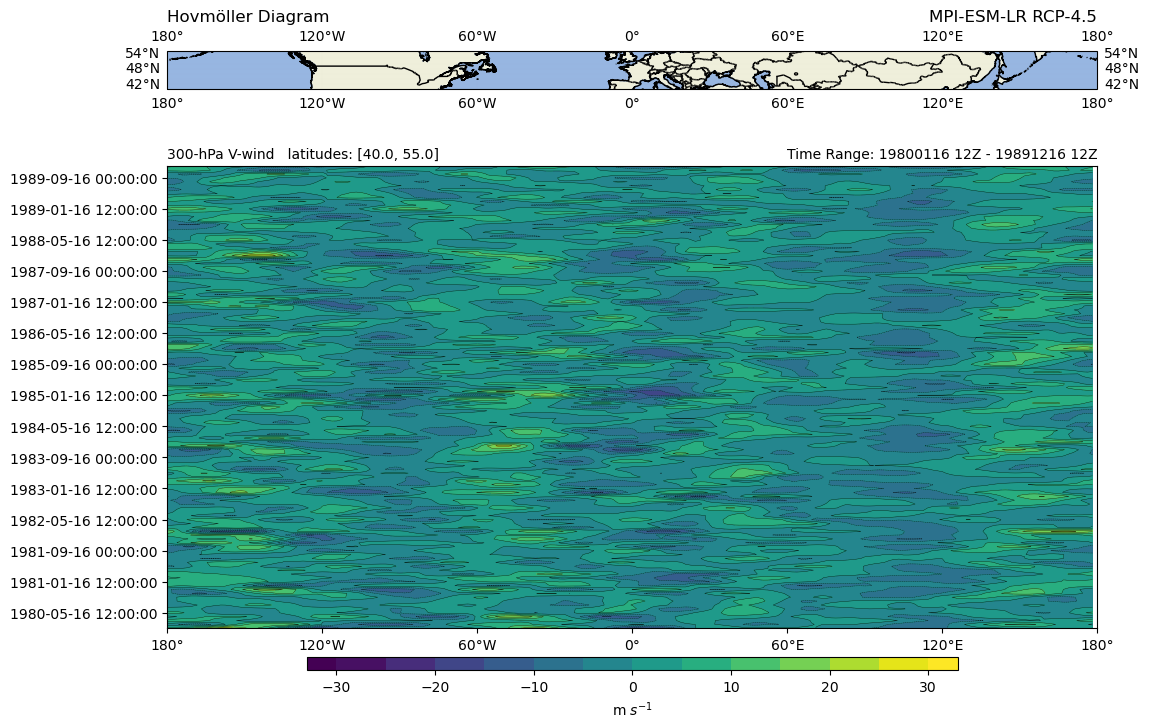
Python Hovmoeller diagram

Software requirements:

• Python 3

• numpy

• xarray

• matplotlib

• cartopy

Example script

Hovmoeller_diagram_with_additional_map.py

#!/usr/bin/env python
# coding: utf-8
'''
DKRZ example

Hovmöller diagram with additional map

A Hovmöller diagram is often used for meterological data. The diagram
shows the contours of a spatial variable in time and space:

    x-axis: longitude or latitude
    y-axis: time

Here for demonstration purposes, we use the variable northward wind, get
the data slice along a specified range of latitudes (40° - 55°) and plot
it against time.

Content

- read netCDF file
- extract slices
- convert pressure levels to height
- create a Hovmöller diagram
- add a map on top of the plot
- save to PNG

-------------------------------------------------------------------------------
2022 copyright DKRZ licensed under CC BY-NC-SA 4.0 <br>
               (https://creativecommons.org/licenses/by-nc-sa/4.0/deed.en)
-------------------------------------------------------------------------------'''
import xarray as xr
import numpy as np
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import cartopy.feature as cfeature

def main():
    plt.switch_backend('agg')

    # Read the CMIP5 atmos historical dataset of the northward wind.
    infile = '../../data/va_Amon_t1.nc'

    ds = xr.open_dataset(infile)

    # The grid of the data contains longitudes from 0° to 360°, but we want to
    # have them from -180° to 180°.
    ds = ds.assign_coords(lon=(((ds.lon + 180) % 360) - 180)).sortby('lon')

    # Select variable **va** from dataset and convert the pressure levels from
    # Pa to hPa, and overwrite plev in the dataset.
    vnwind = ds.va

    levels = ds.plev / 100
    levels.attrs['units'] = 'hPa'

    vnwind['plev'] = levels

    # Select the latitude range to be used and select one pressure level.
    lat_slice = [40., 55.]
    sel_lev = 300

    # Next, get the slices of the data.
    data = vnwind.sel(plev=sel_lev,
                      lat=lat_slice,
                      method='nearest')

    # Compute the weights and the weighted mean over latitude dimension.
    weights = np.cos(np.deg2rad(data.lat))
    weights.name = "weights"

    data_weighted = data.weighted(weights)
    data_weighted_mean = data_weighted.mean('lat')
    data_weighted_mean.name = 'va'

    # Create datetime objects
    vtimes = vnwind.time.values.astype('datetime64[ms]').astype('O')

    # Create the Hovmöller plot and add a small map of the region above it.
    projection = ccrs.PlateCarree()

    fig = plt.figure(figsize=(12, 10), constrained_layout=False)

    # define space for the two plots
    gs = fig.add_gridspec(nrows=4, ncols=1, hspace=0)

    #-- create the small upper map
    ax1 = plt.subplot(gs[0, 0], projection=projection)
    ax1.set_extent([-180., 180., lat_slice[0], lat_slice[1]],
                   crs=ccrs.PlateCarree())
    ax1.add_feature(cfeature.LAND)
    ax1.add_feature(cfeature.OCEAN)
    ax1.add_feature(cfeature.BORDERS)
    ax1.add_feature(cfeature.COASTLINE)
    ax1.gridlines(draw_labels=True, lw=0.01,crs=ccrs.PlateCarree())

    plt.title(u'Hovmöller Diagram', loc='left')
    plt.title('MPI-ESM-LR RCP-4.5', loc='right')

    #-- create lower Hovmoeller diagram
    clevs = np.arange(-30, 31, 5)

    ax2 = fig.add_subplot(gs[1:, 0], sharex=ax1)

    cf = ax2.contourf(vnwind.lon.values, vtimes, data_weighted_mean,
                      clevs,
                      cmap='viridis',
                      extend='both')

    cs = ax2.contour(vnwind.lon.values, vtimes, data_weighted_mean,
                     clevs,
                     colors='k',
                     linewidths=0.25)

    cbar = plt.colorbar(cf,
                        orientation='horizontal',
                        pad=0.05,
                        shrink=0.7,
                        aspect=50,
                        extendrect=True)
    cbar.set_label('m $s^{-1}$')

    ax2.set_xticks([-180, -120, -60, 0, 60, 120, 180])
    ax2.set_xticklabels([u'180\N{DEGREE SIGN}', u'120\N{DEGREE SIGN}W',
                         u'60\N{DEGREE SIGN}W', u'0\N{DEGREE SIGN}',
                         u'60\N{DEGREE SIGN}E', u'120\N{DEGREE SIGN}E',
                         u'180\N{DEGREE SIGN}'])
    ax2.set_yticks(vtimes[4::8])
    ax2.set_yticklabels(vtimes[4::8])

    plt.title(str(sel_lev)+'-hPa V-wind   latitudes: '+str(lat_slice),
              loc='left',
              fontsize=10)
    plt.title('Time Range: {0:%Y%m%d %HZ} - {1:%Y%m%d %HZ}'.format(vtimes[0], vtimes[-1]),
              loc='right',
              fontsize=10)

    plt.savefig('plot_hovmoeller_2.png',
                 bbox_inches='tight',
                 facecolor='white',
                 dpi=100)


if __name__ == '__main__':
    main()

Plot result: