Python plot vectors on maps using different projections#
The drawing of vectors on a map is often difficult when you use a map projection different than PlateCarree. In this notebook we give a brief overview and show what needs to be considered.
Software requirements:
Python 3
numpy
xarray
matplotlib
cartopy
Example script#
vectors_and_map_projections.py
#!/usr/bin/env python
# coding: utf-8
'''
------------------------------------------------------------------------------
DKRZ example
Vectors on different projections
The drawing of vectors on a map is often difficult when you use a map projection
different than PlateCarree. In this notebook we give a brief overview and show
what needs to be considered.
The base plot is a contour fill plot of the surface temperature data over which
the wind vectors are to be plotted.
Content
- PlateCarree
- Orthographic
- NorthPolarStereo/SouthPolarStereo
- Mollweide
- Robinson
-------------------------------------------------------------------------------
2024 copyright DKRZ licensed under CC BY-NC-SA 4.0 <br>
(https://creativecommons.org/licenses/by-nc-sa/4.0/deed.en)
-------------------------------------------------------------------------------
'''
import xarray as xr
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.path as mpath
import cartopy.crs as ccrs
import cartopy.feature as cfeature
import cartopy.util as cutil
def main():
#-- Open example data file
infile = '../../data/rectilinear_grid_2D.nc'
ds = xr.open_dataset(infile)
#-- Assign coordinate and data variables for time step _t_.
lon = ds.lon
lat = ds.lat
t = 0 #-- time index
var = ds.tsurf.isel(time=t)
u = ds.u10.isel(time=t)
v = ds.v10.isel(time=t)
#-- Colormap
cmap = 'Spectral_r'
#-- Coordinate reference systems (CRS)
#
# Read more about 'Understanding the transform and projection keywords' in the
# Cartopy documentation: <br>
# https://scitools.org.uk/cartopy/docs/latest/tutorials/understanding_transform.html
#
# For the data CRS we can use PlateCarree.
data_crs = ccrs.PlateCarree()
#-- Projections
#
# When using map projections the projection CRS has to be used with `plt.subplots()`, `ax.add_subplot()`, `ax.set_global()`, and `ax.set_extent()` (and if needed with the Cartopy features).
#
# The vector plots for various map projections are generated below.
#-- PlateCarree
#
# Map projection CRS for the cylindrical equidistant map projection.
projection = ccrs.PlateCarree()
# Create contour fill plot and overlay the vectors
plt.switch_backend('agg')
fig, ax = plt.subplots(figsize=(8,8), subplot_kw=dict(projection=projection))
ax.add_feature(cfeature.COASTLINE.with_scale('50m'), edgecolor='grey', linewidth=0.5)
ax.gridlines(draw_labels=True, linewidth=0.5, color='gray',
xlocs=range(-180,180,30), ylocs=range(-90,90,30))
ax.set_title('Wind velocity', fontsize=10, fontweight='bold')
cnplot = ax.pcolormesh(lon, lat, var.values,
cmap=cmap,
transform=data_crs)
incr = 2 #-- increment to thin out the vectors
vplot = ax.quiver(lon[::incr], lat[::incr],
u[::incr,::incr].values,
v[::incr,::incr].values,
scale_units='xy',
scale=2,
angles='xy',
transform=data_crs)
vref = ax.quiverkey(vplot, 0.9, 0.905, 20,
r'$20 \frac{m}{s}$',
labelpos='E',
coordinates='figure', zorder=5)
#plt.savefig('plot_matplotlib_vector_rect.png', bbox_inches='tight', dpi=100)
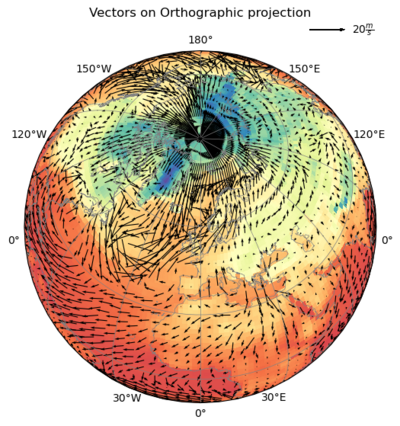
#-- Orthographic projection
#
# To use the Orthographic projection either `ax.set_global()` or `ax.set_extent()` has to be used.
#
# Map projection CRS
projection = ccrs.Orthographic(central_longitude=0.,
central_latitude=60.)
fig, ax = plt.subplots(figsize=(6,6), subplot_kw=dict(projection=projection))
ax.set_global()
ax.set_title('Vectors on Orthographic projection', y=1.08)
ax.add_feature(cfeature.COASTLINE.with_scale('50m'), edgecolor='grey', linewidth=0.5)
ax.gridlines(draw_labels=True, linewidth=0.5, color='gray',
xlocs=range(-180,180,30), ylocs=range(-90,90,30))
cnplot = ax.pcolormesh(lon, lat, var.values,
cmap=cmap,
transform=data_crs)
incr = 2 #-- increment if you want to thin out the vectors
vplot = ax.quiver(lon[::incr], lat[::incr],
u[::incr,::incr].values,
v[::incr,::incr].values,
angles='xy',
scale=200,
color='black',
transform=data_crs)
vref = ax.quiverkey(vplot, 0.91, 1.06, 20,
r'$20 \frac{m}{s}$',
labelpos='E',
coordinates='axes',
color='k')
#-- save to PNG
plt.savefig('plot_matplotlib_vector_ortho.png', bbox_inches='tight', dpi=100)
#-- Change the map projection CRS to zoom into the map.
projection = ccrs.Orthographic(central_longitude=14.,
central_latitude=68.)
# Create the plot
fig, ax = plt.subplots(figsize=(6,6), subplot_kw=dict(projection=projection))
ax.set_extent([-10., 30., 50, 80.], crs=data_crs)
ax.set_title('Vectors on Orthographic projection', y=1.08)
ax.add_feature(cfeature.COASTLINE.with_scale('50m'), edgecolor='grey', linewidth=0.5)
ax.gridlines(draw_labels=True, linewidth=0.5, color='gray',
xlocs=range(-180,180,30), ylocs=range(-90,90,30))
cnplot = ax.pcolormesh(lon, lat, var.values,
cmap=cmap,
transform=data_crs)
incr = 1 #-- increment if you want to thin out the vectors
vplot = ax.quiver(lon[::incr], lat[::incr],
u[::incr,::incr].values,
v[::incr,::incr].values,
angles='xy',
scale=200,
color='black',
transform=data_crs)
vref = ax.quiverkey(vplot, 0.91, 1.06, 20,
r'$20 \frac{m}{s}$',
labelpos='E',
coordinates='axes',
color='k')
#-- save to PNG
plt.savefig('plot_matplotlib_vector_ortho_zoom.png', bbox_inches='tight', dpi=100)
#-- NorthPolarStereo / SouthPolarStereo
#
# Create the two plots using the polar projections at once.
#
#-- north polar
# map projection CRS
projection = ccrs.NorthPolarStereo()
fig = plt.figure(figsize=(8,8))
ax1 = fig.add_subplot(1, 2, 1, projection=projection)
ax1.set_extent([-180., 180., 60., 90.], crs=data_crs)
ax1.set_title('Vectors on NorthPolarStereo projection', y=1.08)
ax1.add_feature(cfeature.COASTLINE.with_scale('50m'), edgecolor='grey', linewidth=0.5)
ax1.gridlines(draw_labels=True, linewidth=0.5, color='gray',
xlocs=range(-180,180,30), ylocs=range(-90,90,30))
cnplot1 = ax1.pcolormesh(lon, lat, var.values,
cmap=cmap,
transform=data_crs)
incr = 2
vplot1 = ax1.quiver(lon[::incr], lat[::incr],
u[::incr,::incr].values,
v[::incr,::incr].values,
angles='xy',
scale=400,
color='black',
transform=data_crs)
vref1 = ax1.quiverkey(vplot1, 0.91, 1.06, 20,
r'$20 \frac{m}{s}$',
labelpos='E',
coordinates='axes',
color='k')
# circular boundary of the map
# (see https://scitools.org.uk/cartopy/docs/v0.15/examples/always_circular_stereo.html)
theta = np.linspace(0, 2*np.pi, 100)
center = [0.5, 0.5]
radius = 0.5
verts = np.vstack([np.sin(theta), np.cos(theta)]).T
circle = mpath.Path(verts * radius + center)
ax1.set_boundary(circle, transform=ax1.transAxes)
#-- south polar
# map projection CRS
projection = ccrs.SouthPolarStereo()
ax2 = fig.add_subplot(1, 2, 2, projection=projection)
ax2.set_extent([-180., 180., -90., -60.], crs=data_crs)
ax2.set_title('Vectors on SouthPolarStereo projection', y=1.08)
ax2.add_feature(cfeature.COASTLINE.with_scale('50m'), edgecolor='grey', linewidth=0.5)
ax2.gridlines(draw_labels=True, linewidth=0.5, color='gray',
xlocs=range(-180,180,30), ylocs=range(-90,90,30))
cnplot2 = ax2.pcolormesh(lon, lat, var.values,
cmap=cmap,
transform=data_crs)
vplot2 = ax2.quiver(lon[::incr], lat[::incr],
u[::incr,::incr].values,
v[::incr,::incr].values,
angles='xy',
scale=400,
color='black',
transform=data_crs)
vref2 = ax2.quiverkey(vplot2, 0.91, 1.06, 20,
r'$20 \frac{m}{s}$',
labelpos='E',
coordinates='axes',
color='k')
# circular boundary of the map
ax2.set_boundary(circle, transform=ax2.transAxes)
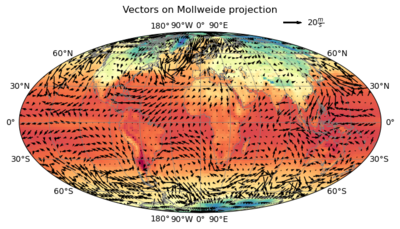
#-- Mollweide
#
# Map projection CRS
projection = ccrs.Mollweide()
# Create the plot
fig, ax = plt.subplots(figsize=(8,8), subplot_kw=dict(projection=projection))
ax.set_global()
ax.set_title('Vectors on Mollweide projection', y=1.08)
ax.add_feature(cfeature.COASTLINE.with_scale('50m'), edgecolor='grey', linewidth=0.5)
ax.gridlines(draw_labels=True, linewidth=0.5, color='gray',
xlocs=range(-180,180,30), ylocs=range(-90,90,30),
x_inline=False, y_inline=False)
cnplot = ax.pcolormesh(lon, lat, var.values,
cmap=cmap,
transform=data_crs)
incr = 3
vplot = ax.quiver(lon[::incr], lat[::incr],
u[::incr,::incr].values,
v[::incr,::incr].values,
angles='xy',
scale=400,
color='black',
transform=data_crs)
vref = ax.quiverkey(vplot, 0.78, 1.05, 20,
r'$20 \frac{m}{s}$',
labelpos='E',
coordinates='axes',
color='k')
#-- save to PNG
plt.savefig('plot_matplotlib_vector_mollweide.png', bbox_inches='tight', dpi=100)
#-- Robinson
#
# Map projection CRS
projection = ccrs.Robinson()
# Create the plot
fig, ax = plt.subplots(figsize=(8,8), subplot_kw=dict(projection=projection))
ax.set_global()
ax.set_title('Vectors on Robinson projection', y=1.08)
ax.add_feature(cfeature.COASTLINE.with_scale('50m'), edgecolor='grey', linewidth=0.5)
ax.gridlines(draw_labels=True, linewidth=0.5, color='gray',
xlocs=range(-180,180,30), ylocs=range(-90,90,30),
x_inline=False, y_inline=False)
cnplot = ax.pcolormesh(lon, lat, var.values,
cmap=cmap,
transform=data_crs)
incr = 3
vplot = ax.quiver(lon[::incr], lat[::incr],
u[::incr,::incr].values,
v[::incr,::incr].values,
angles='xy',
scale=400,
color='black',
transform=data_crs)
vref = ax.quiverkey(vplot, 0.78, 1.08, 20,
r'$20 \frac{m}{s}$',
labelpos='E',
coordinates='axes',
color='k')
if __name__ == '__main__':
main()
Plot result: